Three Different Conceptions Of Group Isomorphisms
The elegance of toggling between equivalent structures
A couple of days ago, I got enormously drunk off of some delicious homemade appletinis made with ingredients from the dollar store and had a highly entertaining discussion with my friend
1. During our lovely 3-hour Zoom rendezvous, I explained to Sai that many times in college, I would get wasted; and, instead of endeavoring to participate in ravenous, unprotected libidinous activities, I would start spouting off about random topics such as the existing gaps in speciation theory.
On one such occasion, after consuming an unhealthy number of IPAs at our underground on-campus watering hole, I gave an intoxicated but highly coherent overview of the First Group Isomorphism Theorem (FGIT) to the young lady who was my fortunate evening accompaniment. Because I attended a college full of thirsty nerds, toward the end of this enthralling elocution, she was about ready to drop her pants to the ground on-the-spot – much to her later chagrin that I was unwilling to seal the deal.
I remember this night in particular, not because of the egoic satisfaction that my flirting skills bring to me (it’s not just straight guys who get validation from seducing dainty damsels), but because, to this day, I still believe it to be one of the most powerful and beautiful theorems in the subfield of algebra2.
Thus, I am going to take some time and space here to discuss three particular perspectives on it.
An Isomorphism of Linear-To-Cyclical Geometry
We’ll start with a simple example that is easy to visualize. Let’s take the group of real numbers under addition and map it to the group characterized by the unit circle in the complex plane. Both these groups are Abelian (i.e., commutative), and it is trivial to show that this function is a homomorphism.
Now, upon determining the kernel to be the set of integers, the resulting homomorphism from the real numbers to its quotient group can be visualized as splitting the number line into equivalent segments of length one; or else reducing it entirely to one continuous segment of length one that represents all the elements.
What naturally follows is that the isomorphism guaranteed by the FGIT…
…takes this line segment of the quotient group and “wraps it around on itself” to form the unit circle.
In this case, the theorem provides a mechanism for changing coordinates: the quotient group shows a way to split the real numbers into identical continuous segments (γ); then, the resulting map (ψ) naturally compresses these equivalent segmented parts into a cyclical geometry. This strategy of changing coordinates is used all the time in engineering and physics problems – for example, when playing around with wave equations – but the foundations behind it are rarely considered.
An Isomorphism of Discrete Rotation-Translation
Our second example will also explore an isomorphism that provides a change in coordinates, but that is much less intuitive, and a lot more sophisticated. In this case, we can consider the Abelian group of integers under addition, but we’re will take an external direct product to make it two-dimensional; in ordinary terms, this is just the integer lattice.
We can construct a super simple map from this lattice back into one dimension. First, we pick random 2D integer coefficients and fix them in place; for simplicity, let’s pick (3,2). Second, using this 2D coefficient, we take linear combinations of all the points in the integer lattice. In other words, the natural function that follows from our choice is:
And it is easy to prove that this function is indeed a homomorphism.
Here is where the juicy part comes in. What does the kernel of this homomorphism look like and what type of quotient group does it produce from the integer lattice? Let’s investigate!
Usually, the special notation <3,2> is given to this particular type of kernel; notice that it can be plotted easily. One can also calculate some plot points by hand from the different elements of the quotient group…
…which reveals that the quotient group takes the kernel (3x + 2y = 0) and translates it according to the various integer constants. From this, we get our isomorphism guaranteed by the FGIT.

In this case, the FGIT provides multiple ways to move from a countable two-dimensional space back into a countable one-dimensional space without losing structural integrity. It does not make automatic sense why this particular quotient group is structurally identical to the integers until you realize that the isomorphism is just a special case of Bézout's identity.
Therefore, when you pick two non-zero, co-prime integers, i.e., their greatest common divisor is 1, a mechanism to hit every ordered pair in the integer plane naturally arises. I don’t exactly know what to call these types of functions, but Bézout homomorphism seems appropriate to me, if you can manage to say that without choking.
Whew!
That required some heavy lifting, but at least we were able to build a geometric intuition about it. We may have a hard time doing that on our next attempt…
An Isomorphism of Spatiodistal Reduction
One of the reasons abstract algebra becomes difficult is that you very quickly start entering into territory that cannot easily be visualized. The most interesting algebraic structures and relationships between them exist far beyond the limitations of two or three dimensions.
For this next example, I won’t even try to create a set of graphics, but will instead try to make a key general observation. Let’s start by defining the following map.
I want to be quite lazy at this point and would prefer, just like a math textbook, to have you, “the reader”, verify that this is indeed a homomorphism. However, my extremely intense former German professor always took points off my homework for skipping steps, so I’ll go ahead and do it.
Finding the kernel of this homomorphism does not cause too much of a sweat either.
Now, at this point, we can go ahead and construct our quotient space, and derive our FGIT-guaranteed isomorphism; however, it is not at all obvious what the geometrical structure of this isomorphism is! – well, at least to plebeians like me and 95% of my fellow human beings who cannot visualize quotient groups in 4D, i.
Somehow the linear combination of this function’s image is fully identical to 2D dimensional real plane under addition. What does that even mean? How is that supposed to be grappled with?
There are a lot of other, similar homomorphisms that you could make from 4D to 2D, or 7D to 3D, or 500D to 43D. What is the point of this? What does it truly reveal about the underlying shapes of these constructions?
I’m not the kind who must sully the allure of pure mathematics with a need for practical applications. That being said, I can think of one immediate advantage to creating these types of maps – and it has to do with the nature of computing the distance between points. The fact is that the higher-dimensional the vector space, the more of a computational nightmare it is to calculate the distance between two points.
Suppose you were trying to run an optimization algorithm across four variables in the middle of an unknown gradient. If you quickly found a robust linear correlation between some of these variables, you could use the FGIT to encounter local maxima way more efficiently than otherwise.
Besides saving on electricity and time, hastening computation is probably a good idea because America might go to war with China this century after Taiwan gets annexed. Then we’ll only be able to rely on the GPUs and TPUs we’ve hoarded in the homeland thus far.
In a future post, I might try to go over some other group structures, such as the finite permutation groups, and the wild equivalences that come from them. The dihedral groups, in particular, are fascinating because they describe many crystalline and chemical structures. At the time in my life when I was studying organic chemistry, my existence disintegrated, and I never quite got a chance to look back.
It feels satisfying to jump back into this particular arena and write some good content about it after a decade of failures and distractions. I often dream that I would be able to teach First Group Isomorphism Theorem things to my children someday. To see the look on my son’s or daughter’s face as they, too, comprehend its unmatched magnificence would be the mark of a life well-lived.
She can tell you how much vodka I consumed; it was a lot, and I enjoyed every sip of it.
Pun heavily intended.






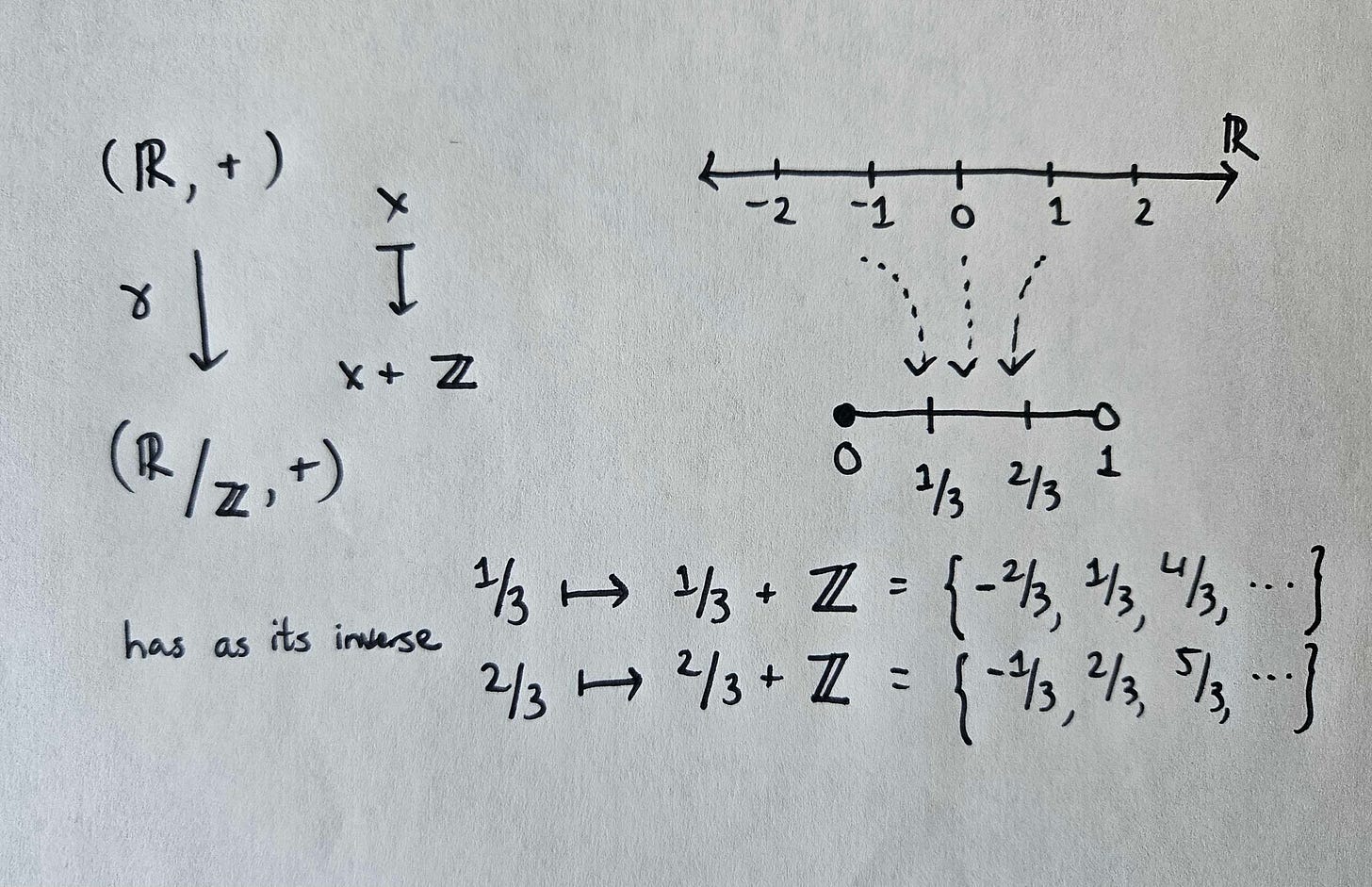



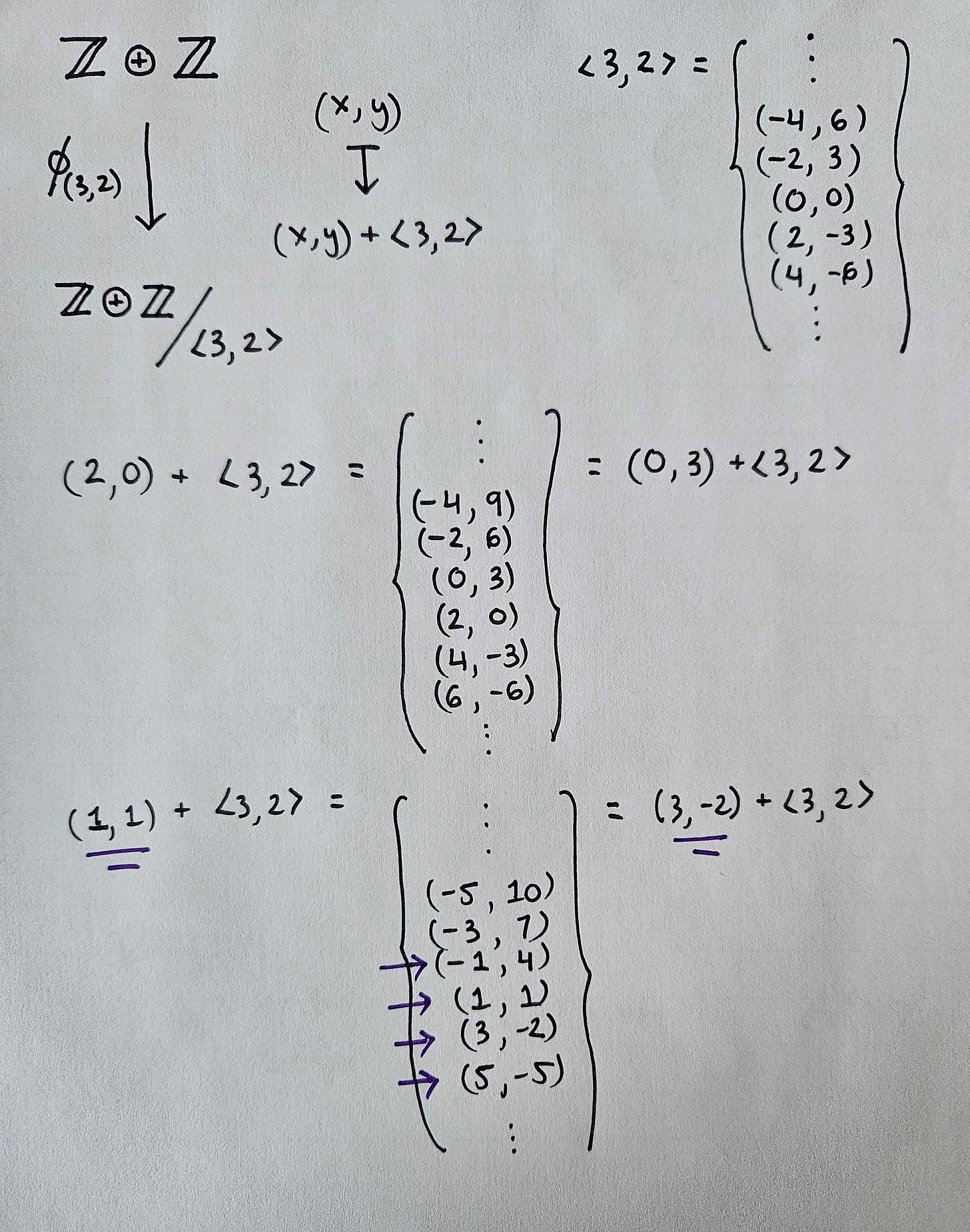





After all the political rabble rousing and talking about talking about talking about vitalism, I for one am thoroughly refreshed learning a bit of actually vital and beautiful piece of abstract math.
I found group isomorphisms so intriguing because they come so close to being an actual mathematical construct of empathy. No wonder that I had to learn about them from you, Rajeev.
I was moved by your vision to teach this to your children someday.